毕达哥拉斯树,又称分形树,是一种无限自相似分形图案。它以其优雅的对称性和几何之美而闻名,在数学和艺术领域都备受推崇。
历史与起源
毕达哥拉斯树最早是由古希腊数学家毕达哥拉斯于公元前6世纪提出的。它被认为是毕达哥拉斯学派的几何符号,代表着宇宙中和谐与比例的重要性。
生成规则
毕达哥拉斯树通过递归规则生成。从一个正方形开始。然后,将正方形分成两个较小的正方形,每个正方形的边长为较大正方形边长的 1/√2。然后,将较大正方形的一个较小正方形的上边缘移动到较小正方形的对角线上,再将其下边缘沿着一条与对角线平行的线移动。这形成了一个 L 形。将此 L 形旋转 90 度并将其放置在较大正方形的另一个较小正方形之上,最终形成一个新的正方形。然后,对新正方形重复相同的过程,无限地产生较小的正方形并形成树状结构。
几何性质
毕达哥拉斯树具有许多引人注目的几何性质:
自相似性:各个尺度的毕达哥拉斯树都与整个树相似。 对称性:树通过一条垂直线和一条水平线对称。 黄金分割:树的各个部分与整体之间的比例遵循黄金分割。 无穷大边长:虽然树的面积有限,但其边长是无限的。 空间填充:树的枝条完全填充了一定的空间,没有空隙。 分形维度:毕达哥拉斯树的分形维度为 2。数学应用
毕达哥拉斯树在数学中有着广泛的应用:
几何定理:它可以用来演示勾股定理。 分形几何:它是分形几何研究中的一个经典例子。 概率论:树的枝条可以用作随机游走的模型。 计算机科学:它被用于开发分形图像和算法。 密码学:树的结构被用作加密算法的基础。艺术表现
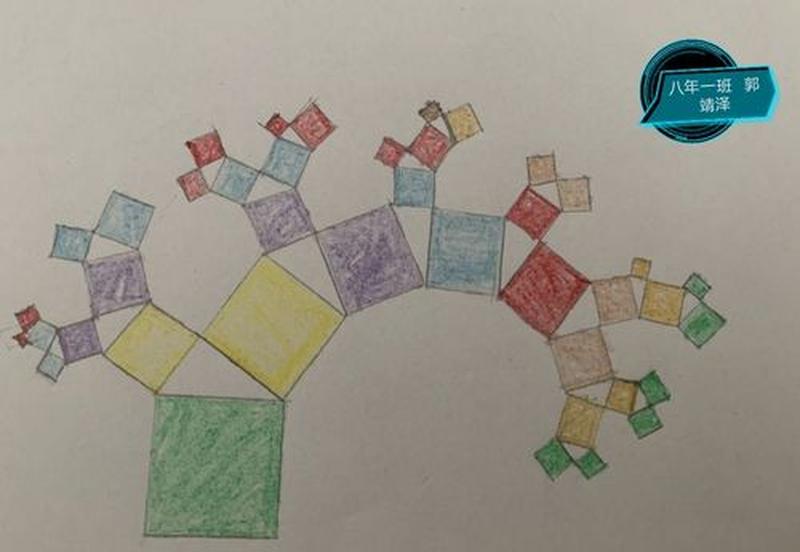
毕达哥拉斯树的美观性使其受到艺术家的喜爱:
绘画和雕塑:艺术家利用树的形状创作出抽象艺术品。 自然摄影:树形结构可以在自然界中找到,例如树枝和闪电。 数字艺术:计算机生成的毕达哥拉斯树被用来 *** 数字艺术和图形。 纹身和首饰:树的图案被用作纹身和首饰设计的元素。文化意义
毕达哥拉斯树超越了数学和艺术领域,在文化中具有重要的象征意义:
和谐与平衡:树的结构代表了宇宙和人类世界中的和谐与平衡。 无穷大和无穷小:树提醒人们无穷大和无穷小的概念。 知识与探索:树的无止境的递归和探索过程象征着求知和智力探索的无限性。 自然与数学:它展示了自然世界中几何和数学原理的共存。