标准差是衡量数据分布分散程度的关键指标,在高级数据分析中扮演着至关重要的角色。小编将从以下 20 个方面深入探讨标准差及其在数据解读中的应用。
标准差的概念
标准差是一种统计度量,它衡量数据值与均值的距离。一个越小的标准差表明数据分布越集中在均值附近,而一个越大的标准差则表明数据分布更加分散。标准差的数学公式为:
```
σ = √(Σ(x - μ)^2 / (n-1))
```
其中:
σ 是标准差
x 是数据值
μ 是均值
n 是数据样本数
正态分布与标准差
在许多实际应用中,数据往往服从正态分布,它是一种对称的钟形分布。在正态分布中,标准差发挥着关键作用:
68% 的数据位于均值正负一个标准差内
95% 的数据位于均值正负两个标准差内
99.7% 的数据位于均值正负三个标准差内
抽样误差与标准差
当从总体中抽取样本时,样本的均值可能会与总体的均值不同。这种差异称为抽样误差,它的程度受样本大小和总体标准差的影响。较小的标准差会导致较小的抽样误差,从而提高样本估计的精度。
假设检验与标准差
假设检验是一种统计 *** ,用于评估样本数据是否支持对总体做出的假设。标准差在假设检验中至关重要,因为它决定了检验统计量的分布。较小的标准差会增加统计显著性,提高拒绝虚无假设的可能性。
置信区间与标准差
置信区间是估计总体参数(例如均值)范围的统计间隔。标准差用于计算置信区间的宽度,较小的标准差会导致更窄的置信区间,从而提高估计的置信度。
标准差在金融分析中的应用
在金融分析中,标准差用于评估投资组合的风险。较小的标准差表示投资组合的波动性较小,较大的标准差表示投资组合的波动性较大。投资者可以利用标准差来衡量风险承受能力并优化投资组合。
标准差在市场研究中的应用
在市场研究中,标准差用于分析消费者行为和市场趋势。通过了解消费者偏好的标准差,企业可以确定目标受众并定制营销策略以满足他们的特定需求。
标准差在医疗保健中的应用
在医疗保健中,标准差用于评估治疗结果的有效性。较小的标准差表明治疗效果更加一致和可预测,较大的标准差则表明治疗效果更加不稳定或不一致。
标准差在教育中的应用
在教育中,标准差用于评估学生的学习成果。较小的标准差表明学生在评估中表现得更加一致,较大的标准差表明学生在评估中表现得更加参差不齐。教师可以利用标准差来识别需要额外支持的学生并调整教学策略。
标准差在科学研究中的应用
在科学研究中,标准差用于评估实验结果的可靠性。较小的标准差表明实验结果更加一致和可重复,较大的标准差则表明实验结果更加不稳定或受其他因素影响。
标准差在制造业中的应用
在制造业中,标准差用于评估生产过程的质量。较小的标准差表明生产过程更加稳定和可控,较大的标准差则表明生产过程存在变异和缺陷的风险。
标准差在服务业中的应用
在服务业中,标准差用于评估客户满意度和服务质量。较小的标准差表明客户体验更加一致和正面,较大的标准差则表明客户体验更加参差不齐或负面。
标准差在体育中的应用
在体育中,标准差用于评估运动员的表现和一致性。较小的标准差表明运动员在比赛中表现得更加稳定和一致,较大的标准差则表明运动员在比赛中表现得更加不稳定或起伏不定。
标准差在多元统计分析中的应用
在多元统计分析中,标准差用于评估自变量对因变量的影响。较小的标准差表明自变量对因变量的影响较小,较大的标准差则表明自变量对因变量的影响较大。
标准差在机器学习中的应用
在机器学习中,标准差用于评估模型的性能。较小的标准差表明模型更加健壮和准确,较大的标准差则表明模型更容易出现过拟合或欠拟合。
标准差在数据挖掘中的应用
在数据挖掘中,标准差用于识别数据中的模式和规律。较小的标准差表明数据点高度相关,较大的标准差则表明数据点高度不相关。
标准差的局限性
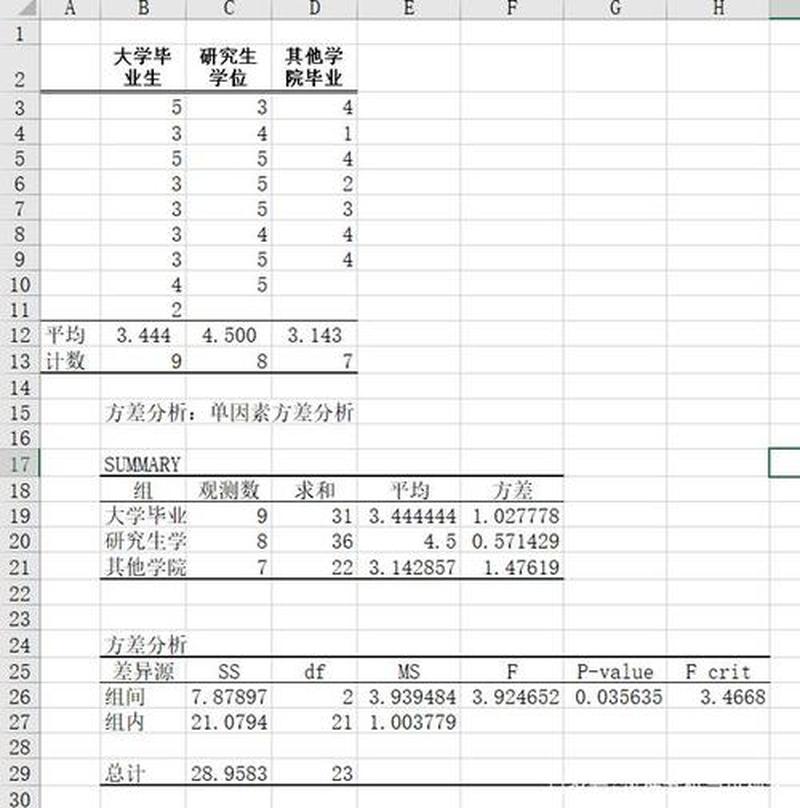
虽然标准差是数据分析中的一个有价值的工具,但它也有一些局限性:
标准差受样本大小的影响,较小的样本往往会导致较大的标准差。
标准差对于异常值敏感,异常值会夸大标准差。
标准差不能区分正向和负向变化。
标准差是数据分析中的一个基本概念,它提供了数据分布分散程度的量化度量。了解标准差的含义和应用至关重要,因为它使数据分析人员能够准确地解释数据、进行假设检验、建模数据并做出明智的决策。通过有效地利用标准差,数据分析人员可以从数据中提取有意义的见解,从而改善决策制定和提高运营效率。